[split] 0.999... equals 1

[Eilonnwy]

And I accept that Eel. I don't understand it. Am I not allowed to question and try to understand

In all seriousness, please don't call me that.

[fr0d0]

And I accept that Eel. I don't understand it. Am I not allowed to question and try to understand

In all seriousness, please don't call me that.

Haha!



Aw ok lovva, as it's U

[Tiberius]

Ok I can dismiss fractions. I can't get the convergence thing still tho'. You may as well call it 1 because there's nothing to add to it to make it 1. But why not just call it '1'?

You may as well, but the point is it is an example of how (going against all common sense) a number can be represented more than one way in the decimal system. As the article says, a lot of students simply refuse to accept the fact because they've always assumed that no two decimal numbers can equal one another.

You could also claim that 2 - 0.9r = 1

Hmm ..I guess I get it

Yay! Indeed, 2 - 0.9r = 1.
Also, 2 - 0.9r = 0.9r given that they are the same thing

Thanks for taking the time to explain it.

No problem. May you go out into the world with a brand new perspective on infinity

[Eilonnwy]

Thinking about that I can see why you could say it's one because there's nothing you can add to it, but conversely, we also know that 0.9r can never logically converge with one.

It doesn't converge, it just is. It's another way of expressing 1 the same way 6/6 is simply another way of expressing 1.

It is logical, it just defies common sense which is why people struggle with it.

[Tiberius]

As I said before, it converges in as much that 2 converges with 2. It literally is the same; if you plot it on a graph you will get the same point.

[Tiberius]

Ok, so it turns out that the third proof I explained (that there is no number between 0.9r and 1) is known as a "continuity" proof. In other words, as I previously stated, for every two numbers that are not the same, there exists a number between them. If not, they are the same number.

The proof by continuity in mathematical form:

A = 0.999...
B = 1

To find the midpoint of any two numbers, you add them together and divide by two. To show you this works:

(1 + 3) / 2 = 4 / 2 = 2.

The midpoint between 1 and 3 is indeed 2.

If you use the same number twice, you get back that number:

(3 + 3) / 2 = 6 / 2 = 3.

Ok, so now put A and B into the equation:

(A + B) / 2

(0.999... + 1) / 2

1.999... / 2 = ?

Well, to do this sum we have to do long division. To make this a little easier to understand, here is a picture of the long division in full swing:

   

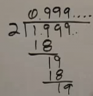
As you can see, you keep diving 19 by 2. 2 goes into 19 9 times, with a 1 remainder. Bringing down the next 9 gives you 19 again, which you divide by 2 to get 9 with 1 remainder, etc etc forever and ever.

So 1.999... / 2 = 0.999...

But wait a minute! That means (going back to our original formula):

(A + B) / 2 = A

Multiply each side by 2 to get rid of the fraction, and you get:

A + B = 2A

Subtract A from each side, and you get:

B = A.

If B = A for A = 0.999... and B = 1, then 1 = 0.999...

Q.E.D

[Amphora]

Very interesting thread.

I don't understand infiniti, but from reading this thread I have gained more knowledge in this particular area.

Amp

[Edwardo Piet]

The continuity proof is my fave. It's fucking awesome. Thanks Adrian.

Am I the only one who things 0.9999999999999999999999...and so on for infinitely, is much more elegant than '1'? Lol.

I guess it's because it's less bland cos I'm so familar with little old '1', and I also think infinitely is cool

So if I'm 99.9r% perfect I'm 100% perfect? Everyone aim for infinity!

EvF

[Retorth]

Evie, you get it too? Woot!

[Edwardo Piet]

I sure do. You can't have infinity +1, and there is no gap between 0.9r and 1, so it's the same number.

The other proofs make sense too. But they make more sense to me, once I know this proof, the continuity one.

EvF